Contoh Regresi Linier Sederhana dengan SPSS
Artikel ini akan mengupas contoh regresi linier sederhana dengan SPSSmenggunakan data regresi yang dipakai seperti pada perhitungan korelasi. Analisis regresi linear sederhana merupakan salah satu metode regresi yang dapat dipakai sebagai alat inferensi statistik untuk menentukan pengaruh sebuah variabel bebas (independen) terhadap variabel terikat (dependen). Uji Regresi linear sederhana ataupun regresi linier berganda pada intinya memiliki beberapa tujuan, yaitu:
- Menghitung nilai estimasi rata-rata dan nilai variabel terikat berdasarkan pada nilai variabel bebas.
- Menguji hipotesis karakteristik dependensi
- Meramalkan nilai rata-rata variabel bebas dengan didasarkan pada nilai variabel bebas diluar jangkaun sample.
Pada analisis regresi sederhana dengan menggunakan SPSS ada beberapa asumsi dan persyaratan yang perlu diperiksa dan diuji, beberapa diantaranya adalah :
- Variabel bebas tidak berkorelasi dengan disturbance term (Error). Nilai disturbance term sebesar 0 atau dengan simbol sebagai berikut: E (U / X) = 0,
- Jika variabel bebas lebih dari satu, maka antara variabel bebas (explanatory) tidak ada hubungan linier yang nyata,
- Model regresi dikatakan layak jika angka signifikansi pada ANOVA sebesar < 0.05, Predictor yang digunakan sebagai variabel bebas harus layak. Kelayakan ini diketahui jika angka Standard Error of Estimate < Standard Deviation,
- Koefisien regresi harus signifikan. Pengujian dilakukan dengan Uji T. Koefesien regresi signifikan jika T hitung > T table (nilai kritis),
- Model regresi dapat diterangkan dengan menggunakan nilai koefisien determinasi (KD = R Square x 100%) semakin besar nilai tersebut maka model semakin baik. Jika nilai mendekati 1 maka model regresi semakin baik,
- Residual harus berdistribusi normal,
- Data berskala interval atau rasio,
- Kedua variabel bersifat dependen, artinya satu variabel merupakan variabel bebas (variabel predictor) sedang variabel lainnya variabel terikat (variabel response) Berikut ini contoh perhitungan regresi linier sederhana menggunakan software SPSS 20.
Proses mulai dengan memilih menu Analyze, kemudian pilih Linear,

Menu Regresi Linear SPSS
Pilih variabel Y sebagai variabel dependen (terikat) dan X1 sebagai variabel independen (bebas) lalu klik tombol OK,

Proses Regresi Linear SPSS
Output SPSS akan menampilkan hasil berupa 4 buah tabel yaitu;
- Tabel variabel penelitian,
- Ringkasan model (model summary),
- Tabel Anova, dan
- Tabel Koefisien.
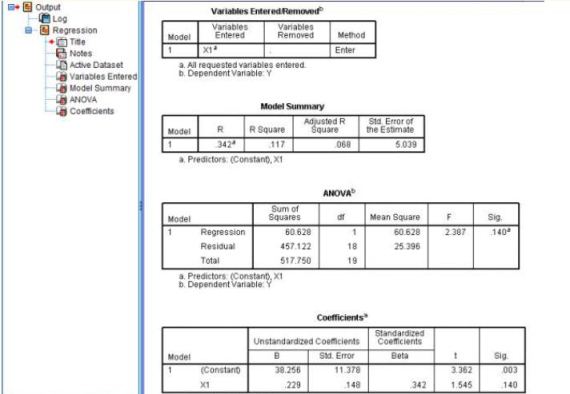
Output Regresi Linear SPSS
Cara membaca output spss hasil uji regresi linier tersebut adalah :
- Tabel pertama menunjukkan variabel apa saja yang diproses, mana yang menjadi variabel bebas dan variabel terikat.
- Tabel kedua menampilkan nilai R yang merupakan simbol dari nilai koefisien korelasi. Pada contoh diatas nilai korelasi adalah 0,342. Nilai ini dapat diinterpretasikan bahwa hubungan kedua variabel penelitian ada di kategori lemah. Melalui tabel ini juga diperoleh nilai R Square atau koefisien determinasi (KD) yang menunjukkan seberapa bagus model regresi yang dibentuk oleh interaksi variabel bebas dan variabel terikat. Nilai KD yang diperoleh adalah 11,7% yang dapat ditafsirkan bahwa variabel bebas X1 memiliki pengaruh kontribusi sebesar 11,7% terhadap variabel Y dan 88,3% lainnya dipengaruhi oleh faktor-faktor lain diluar variabel X1.
- Tabel ketiga digunakan untuk menentukan taraf signifikansi atau linieritas dari regresi. Kriterianya dapat ditentukan berdasarkan uji F atau uji nilai Signifikansi (Sig.). Cara yang paling mudah dengan uji Sig., dengan ketentuan, jika Nilai Sig. < 0,05, maka model regresi adalah linier, dan berlaku sebaliknya. Berdasarkan tabel ketiga, diperoleh nilai Sig. = 0,140 yang berarti > kriteria signifikan (0,05), dengan demikian model persamaan regresi berdasarkan data penelitian adalah tidak signifikan artinya, model regresi linier tidak memenuhi kriteria linieritas.
- Tabel keempat menginformasikan model persamaan regresi yang diperoleh dengan koefisien konstanta dan koefisien variabel yang ada di kolom Unstandardized Coefficients B. Berdasarkan tabel ini diperoleh model persamaan regresi : Y =38,256 + 0,229 X1.
Contoh Regresi Linier Sederhana dengan SPSS
Artikel ini akan mengupas contoh regresi linier sederhana dengan SPSSmenggunakan data regresi yang dipakai seperti pada perhitungan korelasi. Analisis regresi linear sederhana merupakan salah satu metode regresi yang dapat dipakai sebagai alat inferensi statistik untuk menentukan pengaruh sebuah variabel bebas (independen) terhadap variabel terikat (dependen). Uji Regresi linear sederhana ataupun regresi linier berganda pada intinya memiliki beberapa tujuan, yaitu:
- Menghitung nilai estimasi rata-rata dan nilai variabel terikat berdasarkan pada nilai variabel bebas.
- Menguji hipotesis karakteristik dependensi
- Meramalkan nilai rata-rata variabel bebas dengan didasarkan pada nilai variabel bebas diluar jangkaun sample.
Pada analisis regresi sederhana dengan menggunakan SPSS ada beberapa asumsi dan persyaratan yang perlu diperiksa dan diuji, beberapa diantaranya adalah :
- Variabel bebas tidak berkorelasi dengan disturbance term (Error). Nilai disturbance term sebesar 0 atau dengan simbol sebagai berikut: E (U / X) = 0,
- Jika variabel bebas lebih dari satu, maka antara variabel bebas (explanatory) tidak ada hubungan linier yang nyata,
- Model regresi dikatakan layak jika angka signifikansi pada ANOVA sebesar < 0.05, Predictor yang digunakan sebagai variabel bebas harus layak. Kelayakan ini diketahui jika angka Standard Error of Estimate < Standard Deviation,
- Koefisien regresi harus signifikan. Pengujian dilakukan dengan Uji T. Koefesien regresi signifikan jika T hitung > T table (nilai kritis),
- Model regresi dapat diterangkan dengan menggunakan nilai koefisien determinasi (KD = R Square x 100%) semakin besar nilai tersebut maka model semakin baik. Jika nilai mendekati 1 maka model regresi semakin baik,
- Residual harus berdistribusi normal,
- Data berskala interval atau rasio,
- Kedua variabel bersifat dependen, artinya satu variabel merupakan variabel bebas (variabel predictor) sedang variabel lainnya variabel terikat (variabel response) Berikut ini contoh perhitungan regresi linier sederhana menggunakan software SPSS 20.
Proses mulai dengan memilih menu Analyze, kemudian pilih Linear,
 |
| Menu Regresi Linear SPSS |
Pilih variabel Y sebagai variabel dependen (terikat) dan X1 sebagai variabel independen (bebas) lalu klik tombol OK,
 |
| Proses Regresi Linear SPSS |
Output SPSS akan menampilkan hasil berupa 4 buah tabel yaitu;
- Tabel variabel penelitian,
- Ringkasan model (model summary),
- Tabel Anova, dan
- Tabel Koefisien.
 |
| Output Regresi Linear SPSS |
Cara membaca output spss hasil uji regresi linier tersebut adalah :
- Tabel pertama menunjukkan variabel apa saja yang diproses, mana yang menjadi variabel bebas dan variabel terikat.
- Tabel kedua menampilkan nilai R yang merupakan simbol dari nilai koefisien korelasi. Pada contoh diatas nilai korelasi adalah 0,342. Nilai ini dapat diinterpretasikan bahwa hubungan kedua variabel penelitian ada di kategori lemah. Melalui tabel ini juga diperoleh nilai R Square atau koefisien determinasi (KD) yang menunjukkan seberapa bagus model regresi yang dibentuk oleh interaksi variabel bebas dan variabel terikat. Nilai KD yang diperoleh adalah 11,7% yang dapat ditafsirkan bahwa variabel bebas X1 memiliki pengaruh kontribusi sebesar 11,7% terhadap variabel Y dan 88,3% lainnya dipengaruhi oleh faktor-faktor lain diluar variabel X1.
- Tabel ketiga digunakan untuk menentukan taraf signifikansi atau linieritas dari regresi. Kriterianya dapat ditentukan berdasarkan uji F atau uji nilai Signifikansi (Sig.). Cara yang paling mudah dengan uji Sig., dengan ketentuan, jika Nilai Sig. < 0,05, maka model regresi adalah linier, dan berlaku sebaliknya. Berdasarkan tabel ketiga, diperoleh nilai Sig. = 0,140 yang berarti > kriteria signifikan (0,05), dengan demikian model persamaan regresi berdasarkan data penelitian adalah tidak signifikan artinya, model regresi linier tidak memenuhi kriteria linieritas.
- Tabel keempat menginformasikan model persamaan regresi yang diperoleh dengan koefisien konstanta dan koefisien variabel yang ada di kolom Unstandardized Coefficients B. Berdasarkan tabel ini diperoleh model persamaan regresi : Y =38,256 + 0,229 X1.

Silakan tinggalkan komentar anda. DILARANG KERAS menyimpan link blog/web pada komentar dengan tujuan backlink, Spam.